یافتن سطح بین دو منحنی شامل قدر مطلق از مباحث بسیار مهم در کنکور سراسری می باشد که در این فیلم آموزشی به آن پرداخته شده است.
سطح بین دو نمودار قدر مطلق
در این بخش با حل یک مثال، به موضوع چگونگی پیدا کردن سطح بین دو منحنی شامل قدر مطلق خواهیم پرداخت.
تست: سطح بین |2-y=4-|x و |y=|x چه عددی است؟
- 1
- 3
- 6
- 7
گزینه 3 پاسخ صحیح می باشد.
برای حل این مثال دو راه حل وجود دارد.
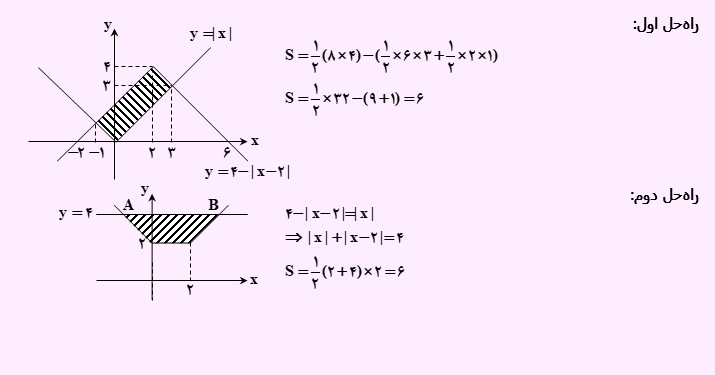
راه حل اول: ابتدا نمودار |y=|x را رسم می کنیم. سپس نمودار |y=4-|x-2 را رسم خواهیم نمود. در نهایت، سطح بین این دو نمودار را با کمک شکل محاسبه خواهیم کرد. مساحت قسمت مورد نظر سوال، با کم کردن مساحت های دو مثلث کوچک از مساحت مثلث بزرگ به دست خواهد آمد (در ویدئو شکل نشان داده شده است). برای مشاهده مراحل راه حل به صورت جزئی می توانید ویدئو آموزشی را مشاهده کنید.
برای محاسبه |y=4-|x-2 و |y=|x می توان، سطح بین دو نمودار y=4 و |2-y=|x|+|x را محاسبه نمود. در حالت کلی برای محاسبه مساحت بین h و f – g، می توان سطح بین f – h و g را حساب نمود. این دو سطح با یکدیگر برابر می باشند. در این مثال، با این کار نمودار به راحتی قابل رسم شده و می توان مساحت را به سادگی حساب نمود. برای مشاهده ادامه و جرئیات راه حل می توانید فیلم آموزشی را مشاهده کنید.
دانستن یک ویژگی از قدر مطلق یا نمودار به شما کمک می کند تا مانند مثال بالا، مساحت و نمودار را ساده تر به دست آورید.
سطح بین دو نمودار قدر مطلق را می توان با توجه به ویژگی های قدر مطلق محاسبه نمود.
به منظور آشنایی بیشتر با موضوع یافتن سطح بین دو منحنی قدر مطلق و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اندازه مساحت بین دو تابع h و f – g، با مقدار مساحت بین تابع های f – h و g برابر می باشد.
با دانستن ویژگی قدر مطلق یا نمودارهای آن می توانید در حل تست های کنکور سراسری با راه حل کوتا ه تر و ساده تری، جواب را پیدا کنید.
به طور کلی به منظور رسم نمودار توابع شامل قدر مطلق، یک دسته از نمودارها با کمک ویژگی قدر مطلق و دسته دیگر با استفاده از بازه بندی قابل حل می باشند. نمودار گلدونی جز دسته ای از نمودارها است که به کمک استفاده از ویژگی قدر مطلق می توان آن را رسم نمود.





