در این فیلم آموزشی در مورد نسبت های مثلثاتی زوایای متمم، مکمل و ساده کردن آن ها توضیح داده شده است.
نسبت های مثلثاتی زوایای مکمل
نسبت های مثلثاتی زوایایی به فرم kΠ±θ (زوایای مکمل):
- نسبت مثلثاتی عوض نمی شود.
- 2kΠ معادل صفر و (2k+1) Π معادل Π است.
- علامت را با توجه به کمان باقی مانده تعیین می کنیم.
مثال) نسبت های مثلثاتی زیر را تعیین کنید؟
sin(3Π-α)=sinα
در مثال بالا 3Π فرد است در نتیجه معادل Π می باشد. همچنین نسبت مثلثاتی عوض نمی شود، لذا سینوس باقی خواهد ماند. Π-α در ربع دوم قرار دارد. علامت سینوس در این ربع مثبت می باشد.
cos(-20Π+α)=cosα
چون 20Π – زوج است، معادل صفر می باشد.
به نمونه تست زیر دقت کنید:
تست) اگر tan20º=α حاصل عبارت زیر کدام است؟
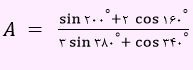
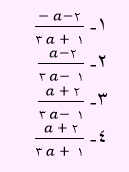
گزینه 1 پاسخ صحیح می باشد.
باید تمام زاویا را بر حسب 20 درجه بنویسم.
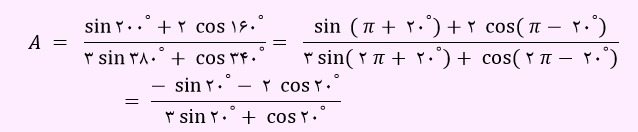
حال صورت مخرج رابطه بالا را بر cos20º تقسیم می نمائیم.
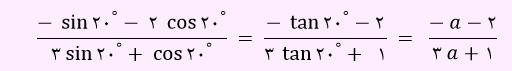
در زوایای مکمل نسبت مثلثاتی عوض نخواهد شد.
نسبت های مثلثاتی زوایای متمم
نسبت های مثلثاتی زوایا به فرم متمم:
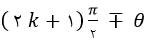
- نسبت مثلثاتی عوض می شود.
- 2kΠ معادل صفر و (2k+1) Π معادل Π است و هر 4×Π/2 معادل 2Π یا همان صفر است.
- علامت را با توجه به کمان باقی مانده تعیین می کنیم.
اگر α و β متمم یکدیگر باشند، داریم:
sinα=cosβ
cosα=sinβ
tanα=cotβ
cotα=tanβ
تست ) اگر α+β=Π/4 حاصل sin22α+sin22β کدام است؟
- 1
- 1/2
- 1/4
- 1/8
گزینه 1 پاسخ صحیح می باشد.
ابتدا طرفین رابطه α+β=Π/4 را در 2 ضرب می کنیم.
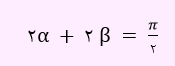
بنابراین زوایای 2α و 2β متمم یکدیگر هستند. لذا sin2α=cos2β .
sin22α+sin22β=cos22β+sin22β=1
به منظور آشنایی بیشتر با نسبت های مثلثاتی زوایای متمم، مکمل و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر دو زاویه متمم یکدیگر باشند، آن گاه سینوس یکی از زوایه ها برابر با کسینوس متمم آن زاویه و تانژانت آن برابر کتانژانت متمم همان زاویه خواهد بود.
در این حالت نکات زیر باید رعایت شود:
1- نسبت مثلثاتی عوض نمی شود.
2- 2kπ معادل صفر و (2k+1) π معادل π است.
3- علامت را با توجه به کمان باقی مانده تعیین می کنیم.





