در این فیلم آموزشی به حل نمونه تست در مورد موضوع احتمال غیر هم شانس خواهیم پرداخت.
نمونه تست احتمال غیر هم شانس
به نمونه تست اول توجه کنید:
تست اول) اعداد 1، 4، 9، 16، 25، 36 را روی 6 وجه مکعبی نوشته و آن را پرتاب می کنیم. اگر احتمال ظاهر شدن هر وجه متناسب با جذر عدد روی آن باشد، احتمال آن که عدد ظاهر شده دو رقمی باشد، کدام است؟
الف) 1/3
ب) 2/3
ج) 4/7
د) 5/7
گزینه د پاسخ صحیح می باشد.
با توجه به اینکه احتمال ظاهر شدن هر وجه متناسب با جذر عدد روی آن است، داریم:
P(1)=k
P(2)=2k
P(3)=3k
P(4)=4k
P(5)=5k
P(6)=6k
جمع احتمال ها باید برابر با یک باشد. یعنی داریم:
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1
k+2k+3k+4k+5k+6k=1 → k= 1/21
تنها سه حالت 16، 25، 36 دو رقمی می باشند. بنابراین احتمال آن که عدد ظاهر شده دو رقمی باشد، به صورت زیر محاسبه خواهد شد:
P(4)+P(5)+P(6)=4k+5k+6k=4/21+ 5/21+ 6/21= 15/21= 5/7
به تست بعدی دقت کنید:
تست دوم) در فضای نمونه ای S={a,b,c,d} اگر P(a)=2 P(b) و P(c)=P(d)= 1/4 باشند. حاصل P(d)/(P(b) کدام است؟
الف) 1/2
ب) 2/3
ج) 1/4
د) 3/2
گزینه د پاسخ صحیح می باشد.
می دانیم مجموع احتمال ها برابر با 1 است. یعنی داریم:
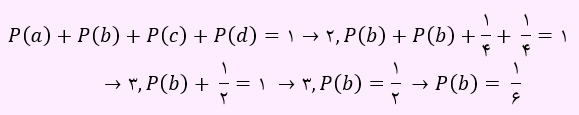
بنابراین حاصلP(d)/P(b) به صورت زیر خواهد بود:
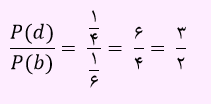
برای آشنایی با نمونه تست های بیشتری از موضوع احتمال غیر هم شانس می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در فضای نمونه ای با احتمال غیر هم شانس، ممکن است تمام پیشامدها دارای احتمال نابرابر باشند، ولی لزوما نباید این اتفاق بیفتد. بلکه در فضای نمونه ای با احتمال غیر هم شانس، نیاز است حداقل دو پیشامد ساده از فضای نمونه ای دارای احتمال نابرابر باشند.
در فضای نمونه ای با احتمال غیر هم شانس، احتمال ها بین صفر و یک بوده و مجموع احتمال ها برابر با یک خواهد بود.





