در این فیلم آموزشی به حل نمونه تست هایی در مورد موضوع پیشامدهای مستقل و وابسته خواهیم پرداخت.
نمونه تست پیشامدهای مستقل و وابسته
به نمونه تست های زیر در مورد موضوع پیشامدهای مستقل و وابسته توجه کنید:
تست اول) در پرتاب یک تاس، پیشامد {6 ,4 ,2} از کدام پیشامد مستقل است؟
1- فرد بودن برآمد
2- اول بودن برآمد
3- مضرب 3 بودن برآمد
4- کمتر از 4 بودن برآمد
گزینه 3 پاسخ صحیح می باشد.
اگر پیشامد {6 ,4 ,2} را A در نظر بگیریم، داریم:

در گزینه 1، پیشامد مربوطه به صورت زیر است:
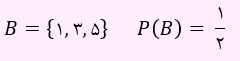
دو پیشامد A و B با یکدیگر هیچ اشتراکی ندارند، لذا مستقل نخواهند بود.
در گزینه 2، پشامد مربوطه به شکل زیر است:

از آنجایی که P(A∩C) با P(A)×P(C) برابر نیست، لذا دو پیشامد مذکور مستقل نخواهند بود.
در گزینه 3، پیشامد مربوطه برابر است با:
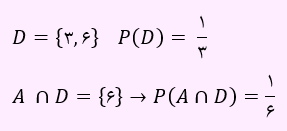
در گزینه 3 ، رابطه زیر برقرار است. لذا دو پیشامد مستقل می باشند.
P(A∩D)=P(A)×P(D)
در گزینه 4، پیشامد به شکل زیر است:
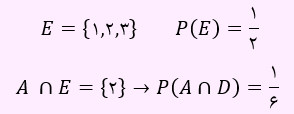
از آنجایی که رابطه زیر در گزینه 4 برقرار است، لذا دو پیشامد مستقل نخواهند بود.
P(A∩E)≠P(A)×P(E)
به نمونه تست دوم و سوم در مورد موضوع پیشامد مستقل و وابسته دقت کنید:
تست دوم) در یک خانواده 4 فرزندی اگر فرزند اول و آخر پسر باشند، با چه احتمالی فرزند دوم و سوم دختر هستند؟
1- 3/16
2- 1/2
3- 1/4
4- 5/16
گزینه 3 پاسخ صحیح می باشد.
جنسیت فرزندان جز پیشامدهای مستقل می باشد، زیرا احتمال این دو پیشامد روی یکدیگر تاثیری نخواهد داشت. بنابراین فرزند دوم با احتمال 1/2 و فرزند سوم نیز با احتمال 1/2 دختر می باشد. لذا فرزند دوم و سوم با احتمال 1/2 × 1/2 یعنی 1/4، دختر خواهد بود.
تست سوم) در پرتاب 3 تاس با هم، با چه احتمالی هر 3 برآمد مضرب 3 نیست؟
1- 1/2
2- 1/6
3- 4/9
4- 8/27
گزینه 4 پاسخ صحیح می باشد.
این 3 پیشامد مستقل از یکدیگر هستند. بنابراین داریم:
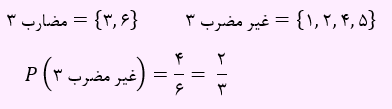
بنابراین احتمال اینکه هر 3 برآمد مضرب 3 نباشند، برابر است با
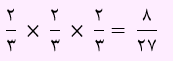
برای مشاهده نمونه تست های بیشتر در مورد موضوع پیشامدهای وابسته و مستقل می توانید به ویدئو آموزشی مراجعه کنید.
سوالات متداول
متمم دو پیشامد مستقل نیز مستقل خواهند بود.
دو پیشامد مستقل حتما با یکدیگر اشتراک خواهند داشت و اشتراک آن ها هیچ گاه تهی نمی باشد.





