در این فیلم آموزشی به بخش اول فصل دو ریاضی 2 تجربی یعنی نیمساز و ویژگی های آن خواهیم پرداخت.
نیمساز و ویژگی های آن
نیمساز یک زاویه دارای ویژگی های زیر می باشد.
- هر نقطه بر روی نیمساز یک زاویه، از دو ضلع آن زاویه به یک فاصله است.
- هر نقطه که از دو ضلع یک زاویه به یک فاصله باشد، بر روی نیمساز آن زاویه قرار دارد.
- ویژگی های نیمساز در شکل زیر نشان داده شده است:

هر نقطه روی نیمساز یک زاویه، از دو ضلع آن زاویه به یک فاصله می باشد.
نمونه تست نیمساز یک زاویه
در این بخش برای فهم بهتر موضوع به حل نمونه تست می پردازیم.
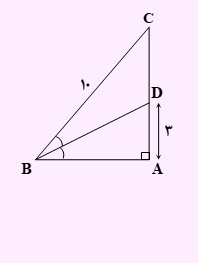
تست) در شکل مقابل، BD نیمساز است. مساحت مثلث BDC کدام است؟
- 30
- 15
- 15/2
- 15/4
گزینه 2 پاسخ صحیح می باشد.
در شکل بالا دو زاویه B1 و B2 با یکدیگر برابر می باشند. چون BD نیمساز است.
اگر از نقطه D، یک خط عمود بر پاره خط BC رسم کنیم، چون نقطه D روی نیمساز BD قرار دارد، اندازه این پاره خط برابر با پاره خط AD یعنی 3 خواهد بود. پس طول ارتفاع مثلث 3 می باشد. حال مساحت مثلث را به صورت زیر حساب خواهیم کرد.
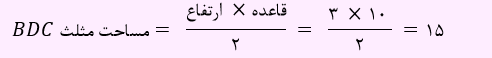
بنابراین مساحت مثلث BDC برابر با 15 می باشد .
به نمونه تست دوم دقت نمائید:
تست: با توجه به شکل مقابل، نقطۀ O (مرکز دایرۀ محاطی مثلث) محل تقاطع …………… در مثلث ABC است.
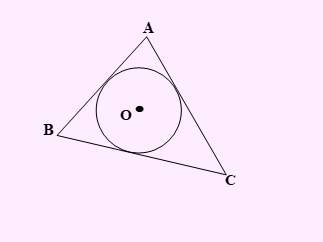
- عمود منصف ها
- نیمسازها
- ارتفاع ها
- میانه ها
گزینه 2 پاسخ صحیح می باشد.
به منظور یادگیری بیشتر موضوع نیمساز یک زاویه و ویژگی های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
نیمساز یک زاویه، نیم خطی است که یک زاویه را نصف خواهد کرد. در واقع هر نقطه بر روی نیمساز یک زاویه، از دو ضلع آن زاویه به یک فاصله خواهد بود.
هر نقطه بر روی نیمساز یک زاویه، از دو ضلع آن زاویه به یک فاصله می باشد.





