در این فیلم آموزشی با ویژگی های اصل ترکیب شامل ویژگی پاسکال و نکات آن آشنا خواهید شد.
ویژگی های اصل ترکیب
اصل ترکیب دارای ویژگی های زیر می باشد:
اگر n عدد طبیعی و k عدد حسابی بین صفر و n باشد، آنگاه:

ویژگی اول بیان می کند که ترکیب k از n با ترکیب (n-k) از n برابر است.

ویژگی 3 بیان می کند که تعداد زیر مجموعه های زوج عضوی با تعداد زیر مجموعه های فرد عضوی برابر بوده و مساوی با نصف تعداد کل زیر مجموعه ها خواهد بود.

به ویژگی شماره 4، ویژگی پاسکال گفته خواهد شد.
اصل ترکیب دارای ویژگی های مهمی می باشد که برای حل نمونه تست ها مورد نیاز می باشد.
نمونه تست ویژگی های اصل ترکیب
به نمونه تست اول توجه کنید:
تست اول) اگر رابطه زیر برقرار باشد، آنگاه برای k چند مقدار به دست می آید؟
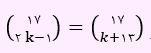
1- 1
2- 2
3- هیچ
4- بی شمار
گزینه 3 پاسخ صحیح می باشد.
می دانیم اگر (n, k1)=(n, k ) آنگاه:
k=k1
یا
k+k1=n
بنابراین با توجه به رابطه زیر داریم:

عدد 14 غیر قابل قبول است. زیرا جمع 14 و 13 برابر با 27 خواهد شد که از عدد 17 بیشتر است.
چون k عددی صحیح نشده است، غیر قابل قبول می باشد.
برای فهم بهتر موضوع به تست زیر توجه فرمایید:
تست دوم) در یک دوره مسابقات بین 12 مدرسه، از هر مدرسه 4 نفر دعوت شده اند. به چند طریق سه دانش آموز که دو به دو غیر هم مدرسه ای باشند می توان انتخاب کرد؟
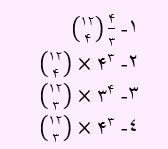
گزینه 4 پاسخ صحیح می باشد.
در ابتدا از بین 12 مدرسه، 3 مدرسه انتخاب خواهیم کرد. سپس هر کدام از این مدارس دارای 4 انتخاب هستند(انتخاب یک دانش آموز از بین 4 نفر).

برای آشنایی بیشتر با موضوع ویژگی های اصل ترکیب، نمونه سوالات تستی و تشریحی آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
جمع ترکیب صفر شی از بین n شی، یک شی از n شی، دو شی از بین n شی تا n شی از بین n شی برابر با دو به توان n خواهد شد. زیرا در واقع این امر مانند این است که زیر مجموعه های صفر عضوی از یک مجموعه n عضوی، زیرمجموعه های یک عضوی، زیر مجموعه های دو عضوی تا زیر مجموعه های n عضوی را با یکدیگر جمع نمائیم که برابر با مجموع تعداد تمام زیر مجموعه ها خواهد بود.
ویژگی پاسکال در اصل ترکیب بیان می کند که جمع ترکیب k از n و k-1 از n برابر است با ترکیب k از n+1.
تعداد زیر مجموعه های زوج عضوی یک مجموعه با تعداد زیر مجموعه های فرد عضوی آن مجموعه برابر بوده و این تعداد مساوی با نصف تعداد کل زیر مجموعه ها می باشد.





