در این فیلم آموزشی با کاربرد توابع نمایی و لگاریتمی و نمونه تست های آن آشنا خواهید شد.
کاربرد تابع نمایی
کاربرد تابع نمایی: در حالت کلی یک تابع به صورت f(x)=kax که در آن (a>0, a≠1) است، مانند تابع نمایی رفتار می کند که در بسیاری از مسائل اقتصادی، طبیعی، مهندسی و … ظاهر می شود.
تست ) نوع خاصی از یک نوع بیماری با 100 باکتری شروع می شود. اگر هر باکتری در مدت نیم ساعت به دو قسمت تقسیم شود، اندازه هر توده باکتری بعد از t ساعت از کدام رابطه به دست می آید؟( t بزرگتر مساوی صفر و کوچکتر مساوی 16 می باشد.)
الف) f(t)=100(2t)
ب) f(t)=100(4t)
ج) f(t)=2t
د) f(t)=4t
گزینه 2 پاسخ صحیح می باشد.
با توجه به صورت سوال، در هر ساعت هر باکتری به 4 باکتری تقسیم می شود. بنابراین در پایان یک ساعت تعداد باکتری 4 برابر، در پایان 2 ساعت تعداد 4×4=42 برابر، در پایان 3 ساعت تعداد 42×4=43 باکتری برابر خواهد شد. لذا در پایان t ساعت، تعداد باکتری 4t برابر می شود.
بنابراین تابعی که تعداد باکتری ها را بعد از t ساعت محاسبه می کند، به صورت زیر خواهد بود.
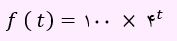
توابع نمایی در بسیاری از مسائل اقتصادی، طبیعی، مهندسی و … کاربرد دارند.
کاربرد توابع لگاریتمی
کاربرد تابع لگاریتمی: ریشتر مقیاسی برای اندازه گیری بزرگی زمین لرزه است که میزان انرژی آزاد شده را نشان می دهد. اگر M میزان بزرگی یک زلزله بر حسب ریشتر و E انرژی آزاد شده آن زلزله در واحد ارگ (Erg) باشد، داریم:
تست) در یک زلزله 8 ریشتری انرژی آزاد شده در واحد ارگ (Erg) چقدر است؟
الف) 1020.8
ب) 1022.8
ج) 1023.8
د) 1024.8
گزینه 3 پاسخ صحیح می باشد.
با توجه به صورت سوال، مقدار M برابر با 8 می باشد. لذا با توجه به فرمول، میزان انرژی آزاد شده را محاسبه خواهیم کرد.

به منظور آشنایی بیشتر با کاربرد توابع نمایی، لگاریتمی و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
کاربرد تابع نمایی بیشتر در مسائلی است که در بازه های زمانی یکسان، یک تابع به یک اندازه رشد یا زوال پیدا می کند.
یکی از مهم ترین کاربردهای تابع لگاریتمی در محاسبه مقدار انرژی آزاد شده در زمین لرزه می باشد. اگر M میزان بزرگی یک زلزله بر حسب ریشتر و E انرژی آزاد شده آن زلزله در واحد ارگ (Erg) باشد، رابطه زیر را خواهیم داشت:
log E= 11⁄8 + 1⁄5 M





