در این فیلم آموزشی با موضوع ترکیب و نمونه تست های آن آشنا خواهید شد.
ترکیب چیست؟
ترکیب: به هر انتخاب r شی از n شی متمایز که در آن ترتیب انتخاب اهمیت نداشته باشد یا به عبارتی به هر زیر مجموعه r عضوی از یک مجموعه n عضوی، یک ترکیب r تایی از n شی می گوییم. تعداد ترکیب های r تایی از n شی متمایز را با نماد C(n,r) نمایش می دهیم و داریم:

مثال 1) از یک مجموعه 5 عضوی قصد داریم یک زیر مجموعه 3 عضوی انتخاب کنیم. این مثال نمونه ای از ترکیب است. زیرا ترتیب قرار گرفتن اهمیتی ندارد.
مثال 2) یک مجموعه 5 عضوی، چند زیر مجموعه 2 عضوی دارد؟
پاسخ این مثال را از طریق رابطه ترکیب به صورت زیر به دست خواهیم آورد:

مثال 3) اگر A={1, 2, 3, 4, 5, 6, 7}، آنگاه مجموعه A دارای چند زیر مجموعه است که :
1- 4 عضوی باشد؟
از این مجموعه 7 عضوی، یک زیر مجموعه 4 عضوی می خواهیم. بنابراین طبق رابطه ترکیب داریم:
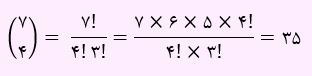
2- 5 عضوی باشد و شامل 1و 2 باشد؟
در این زیر مجموعه 5 عضوی، دو عضو 1 و2 انتخاب شده اند، بنابراین از بین 5 عضو باقی مانده باید 3 عضو دیگر انتخاب نمائیم:
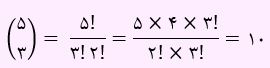
3- 6 عضوی باشد شامل 1 باشد اما شامل 2 نباشد؟
در این زیر مجموعه 6 عضوی، عضو 1 حتما باید باشد. بنابراین 5 زیر مجموعه دیگر باید انتخاب کنیم که انتخاب این 5 زیر مجموعه باید از بین 5 عضو باقی مانده صورت گیرد. زیرا عضو 2 و 1 دیگر داخل اعضا نیستند. لذا داریم:
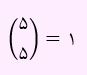
به هر انتخاب r شی از n شی متمایز بدون اهمیت داشتن ترتیب انتخاب ترکیب گفته خواهد شد.
نمونه تست ترکیب
به نمونه تست اول توجه کنید:
تست اول) از بین 5 دانش آموز تجربی و 4 دانش آموز ریاضی به چند طریق می توان 3 نفر انتخاب کرد به طوری که حداقل 2 نفر آن ها رشته ریاضی باشند؟
1- 30
2- 42
3- 34
4- 36
گزینه 3 پاسخ صحیح می باشد.
برای آنکه حداقل 2 نفر رشته ریاضی باشند دو حالت داریم، یا 2 نفر رشته ریاضی و یک نفر رشته تجربی باشد یا هر 3 نفر رشته ریاضی باشند.
پس به این ترتیب داریم:
ابتدا از اصل ضرب استفاده خواهیم کرد و سپس با استفاده از اصل جمع، دو حالت مورد نظر را با یکدیگر جمع خواهیم کرد:
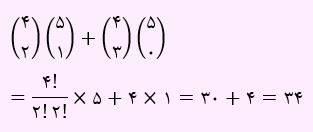
در این سوال، از کلیه اصول جمع، ضرب و ترکیب استفاده شده است.
برای آشنایی بیشتر با موضوع ترکیب، نمونه سوالات تستی و تشریحی آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
جایگشت به نوعی انتخاب محسوب می شود. به منظور انتخاب k شی از بین n شی از جایگشت استفاده خواهد شد. در واقع به هر حالت قرار گرفتن n شی متمایز در کنار هم یک جایگشت از آن اشیا گفته خواهد شد.
به منظور محاسبه تعداد ترکیب های r تایی از n شی متمایز، نیاز است n فاکتوریل را بر حاصل ضرب r فاکتوریل در فاکتوریل تفاضل r از n تقسیم نمائیم.
خیر. در اصل ترکیب ترتیب انتخاب اهمیتی ندارد. در واقع ترکیب عبارت است از انتخاب هر r شی از n شی متمایز که در آن ترتیب انتخاب اهمیتی نداشته باشد. به بیانی دیگر به هر زیر مجموعه r عضوی از یک مجموعه n عضوی، یک ترکیب r تایی از n شی گفته خواهد شد.





