در این فیلم آموزشی به موضوع توابع قدر مطلق، نمودار آن ها و تبدیل تابع قدر مطلق به تابع چند ضابطه ای خواهیم پرداخت.
تابع قدر مطلق
منظور از قدر مطلق یک عدد، مقدار مثبت یا اندازه آن است. به طور مثال قدر مطلق اعداد زیر نوشته شده است.
2 =|2-|
3/7 = |3/7-|
تابع با ضابطه |f(x) = |x ، تابع قدر مطلق نامیده می شود و داریم:
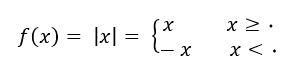
اگر ورودی تابع قدر مطلق عدد مثبت یا صفر باشد، خروجی این تابع برابر با خود آن عدد خواهد شد. اگر ورودی تابع قدر مطلق منفی باشد، خروجی تابع، قرینه آن عدد خواهد شد.
بنابراین تابع قدر مطلق، یک تابع دو ضابطه ای است. نمودار تابع قدر مطلق به صورت زیر است:

تابع قدر مطلق، یکی از انواع توابع دو ضابطه ای می باشد.
تبدیل تابع قدر مطلق به تابع چند ضابطه ای
تبدیل تابع قدر مطلق به یک تابع چند ضابطه ای: در تعریف تابع قدر مطلق x، به جای x هر عبارت دیگری می تواند قرار گیرد.
مثال) تابع |y = |2x-6 را چند ضابطه ای کنید؟
قدر مطلق هر عبارتی، اگر آن عبارت بزرگتر مساوی صفر باشد، برابر با خود آن عبارت، و اگر عبارت مربوطه کوچکتر از صفر باشد، مساوی با قرینه آن عبارت خواهد شد. پس برای تابع داده شده داریم:
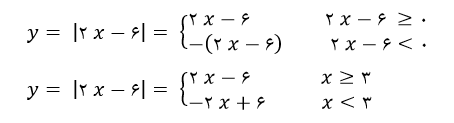
برای آشنایی بیشتر با تابع قدرمطلق و روش رسم نمودار آن ویدئوی آموزشی این جلسه را مشاهده نمایید.
سوالات متداول
تابع قدر مطلق، تابعی است با ضابطه|f(x) = |x . در واقع تابع قدر مطلق یک تابع دو ضابطه ای می باشد.در تابع قدر مطلق، اگر ورودی عدد مثبت یا صفر باشد، خروجی تابع قدر مطلق برابر با خود آن عدد می شود. اگر ورودی تابع قدر مطلق یک عدد منفی باشد، خروجی تابع قدر مطلق، مساوی با قرینه آن عدد خواهد شد.
قدر مطلق یک عدد، برابر با مقدار مثبت یا اندازه آن عدد خواهد بود. به طور مثال قدر مطلق عدد 3- یعنی |3-| مساوی با 3 خواهد شد.
ریشه داخل قدر مطلق عددی است که نمودار تابع را بر روی محور x ها قطع خواهد کرد.





