در این فیلم آموزشی به حل تست هایی از قوانین و قضایای احتمال خواهیم پرداخت.
نمونه تست قوانین و قضایای مهم احتمال
نکته: تعداد مضارب k( اعداد بخش پذیر بر k) از مجموعه {n,…..,1,2,3} برابر است با :[ n/k]
حال به حل نمونه تست خواهیم پرداخت:
تست اول) از مجموعه {1, 2, 3, ……, 500} عددی به تصادف انتخاب می کنیم. با کدام احتمال این عدد بر 4 بخش پذیر است اما مضرب 6 نیست؟
1- 0.168
1- 0.162
3- 0.178
4- 0.172
گزینه 1 پاسخ صحیح می باشد.
اگر بخش پذیری بر 4 را برابر با A و مضرب 6 بودن را B در نظر بگیریم، صورت سوال P(A-B) را خواسته است. بنابراین داریم:
P(A-B)=P(A)-P(A∩B)
اعدادی هم بر 4 و هم بر 6 بخش پذیر هستند که مضرب 12 باشند. لذا داریم:

به نمونه تست دوم توجه فرمایید:
تست دوم) از مجموعه اعداد {101,102,103,…,250} عددی به تصادف انتخاب می کنیم. با کدام احتمال این عدد لااقل بر یکی از اعداد 4 یا 5 بخش پذیر است؟
1- 0.4
2- 0.42
3- 0.58
4- 0.6
گزینه 1 پاسخ صحیح می باشد.
در این سوال، بخش پذیری بر 4 را برابر با A و بخش پذیری بر 5 را برابر با B در نظر می گیریم. صورت سوال P(A ∪B) را خواسته است. بنابراین داریم:
P(A∪B)=P(A)+P(B)-P(A∩B)
چون اعداد از 101 شروع شده است، برای محاسبه احتمال بخش پذیری، باید احتمال از 1 تا 250 را حساب کرده و سپس احتمال 1 تا 100 را از آن کم کنیم. یعنی داریم:
احتمال بخش پذیری بر 4:
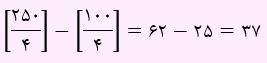
احتمال بخش پذیری بر 5:
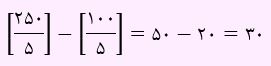
اگر عددی هم بر 4 و هم بر 5 بخش پذیر باشد، یعنی باید بر 20 بخش پذیر باشد.
احتمال بخش پذیری هم بر 4 و هم بر 5 یعنی بر 20:
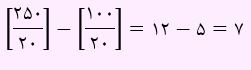
حال برای محاسبه P(A∪B) داریم:
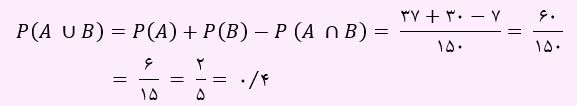
برای ملاحظه نمونه تست های بیشتر در مورد موضوع قوانین احتمال می توانید فیلم آموزشی را مشاهده کنید.
سوالات متداول
اگر دو پیشامد ناسازگار باشند، احتمال اجتماع دو پیشامد برابر با حاصل جمع احتمال هر کدام از پیشامدها است. زیرا اشتراک دو پیشامد ناسازگار مساوی با تهی می باشد.
برای محاسبه احتمال اجتماع دو پیشامد، احتمال اشتراک دو پیشامد را از مجموع احتمال دو پیشامد کم می نمائیم.
فرض کنید A و B دو پیشامد باشند. برای محاسبه احتمال تفاضل پیشامد B از A، باید احتمال اشتراک دو پیشامد را از احتمال پیشامد A کم کنیم.





