در این فیلم آموزشی با موضوع روش های استدلال و اثبات قضایا شامل برهان خلف (اثبات غیر مستقیم) آشنا خواهید شد.
برهان خلف ( اثبات غیر مستقیم) چیست؟
در ابتدا موضوع برهان خلف یا اثبات غیر مستقیم را توضیح خواهیم داد. عکس بسیاری از قضایا با برهان خلف اثبات می شوند. در واقع در برهان خلف از فرض خلف شروع خواهیم کرد. مسائلی که معمولا در مورد اعداد گنگ مطرح می شود به کمک برهان خلف حل خواهند شد.
برهان خلف ( اثبات غیر مستقیم) : در این روش فرض می کنیم حکم درست نباشد ( فرض خلف) و به یک تناقض یا به یک نتیجه غیر ممکن می رسیم و به این ترتیب فرض خلف باطل و درستی حکم ثابت می شود.
مثال) در شکل مقابل AD نیمساز زاویه A است و BD≠DC. نشان دهید AB≠AC
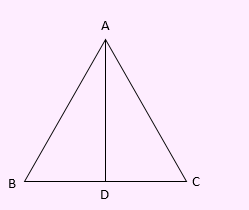
برهان خلف: فرض کنیم AB = AC. در این صورت مثلث ABC متساوی الساقین است و دو مثلث ABD و ACD به حالت “ض ز ض” هم نهشت هستند، پس BD = DC که این مطلب خلاف فرض اولیه است. بنابراین فرض خلف باطل است یعنی AB≠AC .
در برهان خلف (اثبات غیر مستقیم) فرض می کنیم حکم درست نباشد و به یک تناقض می رسیم.
نمونه تست برهان خلف (اثبات غیر مستقیم)
به نمونه تست زیر توجه کنید:
تست) اثبات کدام قضیه زیر احتیاج به روش برهان خلف ندارد؟
- عدد 2∨ عددی گنگ است.
- از یک نقطه خارج یک خط فقط یک عمود می توان بر آن خط وارد کرد.
- اگر n∈N و n2 فرد باشد، در این صورت n نیز فرد است.
- حاصل ضرب دو عدد فرد، عددی فرد است.
گزینه 4 پاسخ صحیح است.
گزینه های 1، 2و 3 با کمک برهان خلف ثابت خواهند شد. برای اثبات گزینه 4 نیاز به برهان خلف نبوده و به صورت مستقیم قابل اثبات می باشد.
برای یادگیری بیشتر موضوع برهان خلف (اثبات غیر مستقیم) و نکات تستی آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در روش برهان خلف ( اثبات غیر مستقیم)، فرض می کنیم حکم درست نباشد (فرض خلف) و به یک تناقض یا به یک نتیجه غیر ممکن خواهیم رسید. به این ترتیب فرض خلف باطل و درستی حکم اثبات خواهد شد.
برهان خلف (اثبات غیر مستقیم) یکی از روش هایی است که به منظور اثبات قضایا می توان از آن کمک گرفت.





