در این فیلم آموزشی در مورد معادلات لگاریتمی و روش حل آن ها توضیح داده شده است.
معادلات لگاریتمی و روش حل آن ها
معمولا معادلات لگاریتمی بدین صورت است که به تساوی دو لگاریتم می انجامد و هنگامی که معادله حل می شود، باید حتما چک نمود جایی از معادله اولیه تعریف نشده نشود. بنابراین شرط دامنه معادلات لگاریتمی بسیار مهم است که در انتهای کار باید حتما چک گردد.
با توجه به یک به یک بودن تابع لگاریتم می توان نوشت:
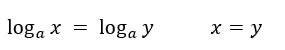
در حل معادلات لگاریتم باید به دامنه توجه کنیم:
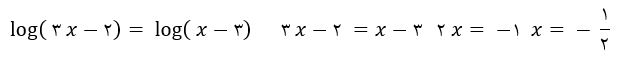
x=-1/2 غیر قابل قبول می باشد. زیرا هر دو عبارت x-3 و 3x-2 منفی می شوند.
در حل معادلات لگاریتمی شرط دامنه معادلات لگاریتمی را حتما باید چک نمود.
نمونه تست معادلات لگاریتمی
به نمونه تست اول توجه کنید:
تست اول ) معادله زیر چند ریشه دارد؟
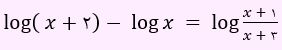
الف) یک
ب) دو
ج) صفر
د) بی شمار
گزینه 3 پاسخ صحیح می باشد.
ابتدا تفریق داده شده را به صورت تقسیم خواهیم نوشت:
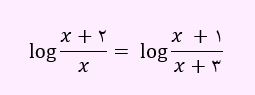
بنابراین مبناها برابر شد و داریم:

مقدار x=-3/2، عبارت logx را منفی کرده، لذا غیر قابل می باشد و معادله جواب ندارد.
به نمونه تست دوم توجه کنید:
تست دوم) مجموع ریشه های معادله log2x+2logx2=3 کدام است؟
الف) 1
ب) 2
ج) 3
د) 6
گزینه 4 پاسخ صحیح می باشد.
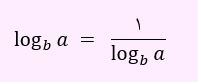
logab و logba قرینه یکدیگر می باشند. اگر log2x را a در نظر بگیریم، logx2 طبق نکته ذکر شده برابر با 1 تقسیم بر a خواهد بود. بنابراین معادله به صورت زیر می باشد:
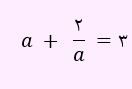
طرفین رابطه را در a ضرب می کنیم.
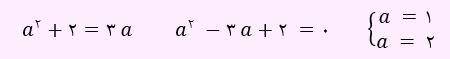
پس log2x برابر یک یا دو می باشد.
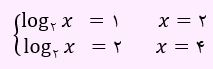
لذا مجموع ریشه های معادله مساوی با 6 خواهد شد.
به منظور یادگیری بیشتر معادلات لگاریتمی و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
خیر. ممکن است تعدادی از جواب ها قابل قبول نباشند. زیرا بعد از به دست آوردن ریشه ها باید چک نمود که جواب های به دست آمده در شرط دامنه صدق کنند.
در اکثر مواقع، معادلات لگاریتمی بدین صورت می باشند که به تساوی دو لگاریتم خواهد انجامید. در این حالت، با توجه به یک به یک بودن تابع لگاریتم می توان جواب را یافت.





