در این فیلم آموزشی با موضوع عبارات رادیکالی، ریشه و توان آشنا خواهید شد.
عبارات رادیکالی چه عباراتی هستند؟
تذکر: هر تساوی توانی را می توانیم به صورت یک تساوی رادیکالی بنویسیم و برعکس:
مثال) تساوی های زیر مثال هایی از نکته بالا می باشند:

نتیجه: از تذکر بالا نکات زیر نتیجه گرفته خواهد شد:
1- هر عدد مثبت دارای 2 ریشه دوم است که قرینه یکدیگر هستند.
2- هر عدد مثبت دارای 2 ریشه چهارم است که قرینه یکدیگر هستند.
3- به طور کلی هر عدد مثبت دارای 2 ریشه زوجم است که قرینه یکدیگر هستند.
مثال) ریشه دوم، چهارم و ششم اعداد زیر بیان شده است:
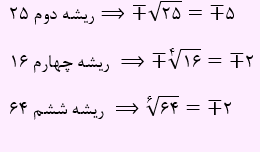
هر تساوی توانی را می توان به صورت یک تساوی رادیکالی نوشت.
نمونه تست اتحادهای مثلثاتی
تذکر: اعداد منفی، ریشه دوم یا چهارم ( به طور کلی ریشه زوج) ندارند.
نکته: به دو تساوی زیر دقت کنید:
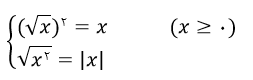
توجه کنید که همین مطالب در مورد فرجه های زوج دیگر نیز برقرار است.
نکته 1: هر عدد مثبت یا منفی دارای 1 ریشه سوم است که با آن عدد هم علامت است.
نکته 2: هر عدد مثبت یا منفی دارای 1 ریشه پنجم است که با آن عدد هم علامت است.
نکته 3: به طور کلی هر عدد تنها یک فرجه فرد دارد که با آن عدد هم علامت می باشد.
مثال) هر یک از اعداد زیر تنها یک فرجه فرد ذکر شده را دارا هستند:
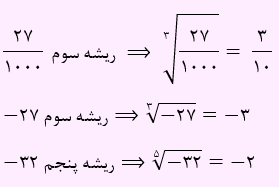
به تست زیر توجه فرمایید:
تست اول) اگر m,n ∈N اعداد متوالی باشند، به طوری که m<∛103<n حاصل m+n کدام است؟
1- 5
2- 7
3- 9
4- 11
گزینه 3 پاسخ صحیح می باشد.
عبارت 103∛ بین دو عبارت 64∛ و 125∛ قرار دارد. بنابراین عبارت 103∛ بین دو عدد 4 و 5 قرار خواهد گرفت. لذا حاصل m+n برابر با 4+5 یعنی 9 خواهد شد.
برای آشنایی بیشتر با موضوع عبارات رادیکالی ریشه، توان و نمونه سوالات تستی آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در حالت کلی، هر عدد مثبت دارای 2 ریشه زوجم می باشد که این دو ریشه زوجم قرینه یکدیگر هستند.
خیر، اعداد منفی ریشه دوم، چهارم، ششم و به طور کلی هیچ ریشه زوجی ندارند.
در حالت کلی، هر عدد چه مثبت و چه منفی، دارای تنها یک فرجه فرد است که فرجه فرد مذکور با آن عدد هم علامت خواهد بود.





