در این فیلم آموزشی به مبحث هندسه مختصاتی شامل نقطه، خط، فاصله دو نقطه از هم و فاصله نقطه از خط خواهیم پرداخت.
فاصله دو نقطه از یکدیگر
هندسه مختصاتی از مباحثی است که از آن در کنکور سراسری به احتمال بسیار زیادی سوال طرح خواهد شد. در این بخش با فاصله دو نقطه از یکدیگر آشنا خواهید شد.
فاصله دو نقطه A(α1, β1) و B(α2, β2) در صفحه از یکدیگر برابر است با جذر مجموع تفاضل عرضها به توان دو و تفاضل طول ها به توان دو. در حقیقت فاصله دو نقطه A(α1, β1) و A(α2, β2) در صفحه از یکدیگر از طریق رابطه زیر محاسبه خواهد شد:

در حالت خاص فاصله A(α, β) تا مبدا مختصات برابر با رابطه زیر می باشد.
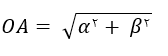
نکته: فاصله دو نقطه روی محور طول ها برابر با اختلاف طول آنهاست. در واقع برای فاصله دو نقطه A(α1, 0) و B(β1, 0) رابطه زیر را خواهیم داشت.
AB=|α1-α2|
فاصله دو نقطه روی محور عرض ها برابر با اختلاف عرض آنهاست. در واقع برای فاصله دو نقطه A(0, β1) و B(0, β2) رابطه زیر را خواهیم داشت.
AB=|β1-β2|
در حقیقت فاصله دو نقطه از یکدیگر به رابطه فیثاغورث باز می گردد. حال برای درک بیشتر موضوع به حل تست می پردازیم.
فاصله دو نقطه از یکدیگر مساوی است با جذر مجموع تفاضل عرض ها به توان دو و تفاضل طول ها به توان دو .
نمونه تست فاصله دو نقطه از یکدیگر
در این بخش به حل نمونه تست هایی در مورد فاصله دو نقطه از یکدیگر می پردازیم:
تست 1) اگر A( 1 , 3)، B(-1 , 2)، C(5 , -5) سه راس یک مثلث باشند، کدام گزینه درست است؟
- مثلث در راس A قائمه است.
- مثلث در راس B قائمه است.
- مثلث در راس C قائمه است.
- مثلث متساوی الساقین است.
گزینه 1 پاسخ صحیح می باشد.
ابتدا فاصله نقاط از یکدیگر، یعنی طول اضلاع را مطابق با روابط زیر حساب می کنیم.
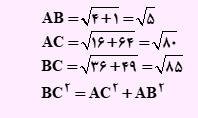
چون هیچ کدام از اضلاع با یکدیگر برابر نمی باشند، پس مثلث از نوع متساوی الساقین و … نمی باشد. رابطه فیثاغورث در این مثلث برقرار است.
بنابراین مثلث در راس A قائمه است. لذا گزینه یک پاسخ صحیح می باشد.
به نمونه تست دوم توجه کنید:
تست 2) اگر (1-, 3)A و (4, 1-)B دو راس مقابل یک مربع باشند، مساحت مربع چه عددی است؟
- 2
- 41/4
- 41
- 41/2
گزینه 4 پاسخ صحیح می باشد.
چون A( 3 , -1) و B(-1 , 4) دو راس مقابل در مربع هستند، بنابراین فاصله این دو نقطه از یکدیگر برابر با قطر مربع می باشد. لذا قطر و مساحت مربع از طریق رابطه زیر محاسبه می شود.
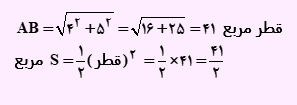
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع هندسه مختصانی و فاصله دو نقطه از یکدیگر ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر دو نقطه روی محور عرض ها قرار گرفته باشند، فاصله آن ها از یکدیگر مساوی با اختلاف عرض آنهاست.
فرض کنید A(α, β) یک نقطه روی صفحه باشد. فاصله نقطه مذکور تا مبدا مختصات برابر است با جذر مجموع توان دوم مختصات نقطه مذکور.
فاصله دو نقطه در صفحه از یکدیگر برابر است با جذر مجموع تفاضل عرضها به توان دو و تفاضل طول ها به توان دو.





