در این فیلم آموزشی با موضوع احتمال غیر هم شانس و نکات آن آشنا خواهید شد.
احتمال غیر هم شانس چیست؟
احتمال غیر هم شانس: هر گاه حداقل دو پیشامد ساده از فضای نمونه ای S={S1,S2 ,…,Sn} احتمال نابرابر داشته باشند، S را فضای نمونه ای با احتمال غیر هم شانس می گوییم.
ویژگی های احتمال غیر هم شانس: در فضای نمونه ای غیر هم شانس S={S1,S2 ,…,Sn} با پیشامد K عضوی A={a1,a2 ,…,ak} ، داریم:
1) 0 ≤ P(A)≤1
2) P(S)=1 ⇒P(S1) + P(S2) + P(S3) +⋯+ P(Sn)=1
3) P(A)= P(a1) + P(a2) + P(a3) +⋯+ P(ak)
هرگاه حداقل دو پیشامد ساده از فضای نمونه ای دارای احتمال نابرابر باشند، به فضای نمونه ای ، فضای نمونه ای با احتمال غیر هم شانس گفته خواهد شد.
نمونه تست احتمال غیر هم شانس
حال برای آشنایی با تست های کنکور سراسری به حل تست خواهیم پرداخت.
تست اول) اگر S={a,b,c,d} و داشته باشیم P(b)= 1/3، P({b,d})= 1/2 و P ({b,c}= 2/3. مقدار P(a) کدام است؟
1- 1/3
2- 1/6
3- 2/3
4- 5/6
گزینه 2 پاسخ صحیح می باشد.
با توجه به P({b,d})= 1/2 داریم:

با توجه به داریم:
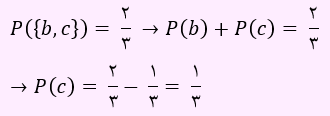
مجموع احتمال ها برابر با 1 است. بنابراین داریم:
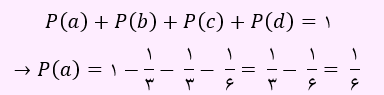
لذا مقدار P(a) برابر با 1/6 به دست آمد.
به دو تست بعدی توجه فرمایید:
تست دوم) چهار دونده a، b، c و d در یک مسابقه شرکت کرده اند. به طوری که برد a سه برابر b ، احتمال برد b نصف احتمال c و دونده های c و d هم شانس هستند. احتمال برنده شدن a یا d کدام است؟
1- 2/5
2- 3/8
3- 1/4
4- 5/8
گزینه 4 پاسخ صحیح می باشد.
طبق صورت سوال، احتمال ها به صورت زیر هستند:
P(a)=3 P(b)
P(b)=1/2 P(c)
P(c)=3 P(d)
جمع احتمال ها برابر با 1 است . یعنی داریم:
P(a)+P(b)+P(c)+P(d)=1
حال، تمام احتمال ها را بر حسب احتمال d خواهیم نوشت:
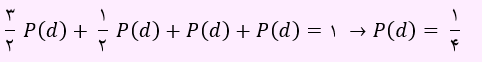
بنابراین P(a) برابر با 3/2 × 1/4 یعنی 3/8 خواهد شد.
لذا احتمال برنده شدن a یا d به صورت زیر خواهد بود:
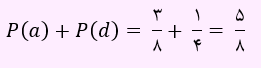
تست سوم) تاسی به گونه ای ساخته شده است که احتمال وقوع هر عدد زوج سه برابر احتمال وقوع هر عدد فرد است. در یک بار پرتاب این تاس، احتمال وقوع عدد بزرگتر از 3 کدام است؟
1- 1/2
2- 2/3
3- 5/12
4- 7/12
گزینه 4 پاسخ صحیح می باشد.
با توجه به سوال داریم:
P(زوج)=3 P (فرد)
P (فرد) را برابر با k در نظر می گیریم. بنابراین P(زوج) مساوی با 3 k خواهد شد.
جمع احتمال ها برابر با 1 است. یعنی داریم:
P(1) + P(2) + P(3) + P(4) + P(5) + P(6)=1 →k + 3k + k + 3k + k + 3k=1 →k= 1/12
احتمال وقوع عدد بزرگتر از 3 به صورت زیر به دست خواهد آمد:
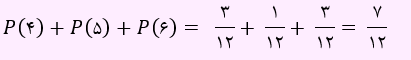
برای آشنایی بیشتر با موضوع احتمال غیر هم شانس و ویژگی های آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
یک فضای نمونه ای را در نظر بگیرید. هر گاه حداقل دو پیشامد ساده از این فضای نمونه ای دارای احتمال نابرابر باشند، به فضای نمونه ای مذکور، فضای نمونه ای با احتمال غیر هم شانس گفته می شود.
در فضای نمونه ای غیر هم شانس، با پیشامد K عضوی، احتمال مجموعه برابر با مجموع احتمال اعضا آن می باشد.
خیر. نیازی به نابرابری احتمال تمام پیشامدها نمی باشد. بلکه نیاز است حداقل دو پیشامد ساده از این فضای نمونه ای دارای احتمال نابرابر باشند.





