در این فیلم آموزشی تابع لگاریتم و نمودار آن توضیح داده شده است.
تابع لگاریتم و ویژگی های آن
تعریف تابع لگاریتم: وارون تابع نمایی f(x)=ax را تابع لگاریتم می گوییم و با نماد f-1(x)=logax نشان می دهیم.
f(x)=ax ↔ f-1(x)=logax
مثال: وارون تابع f(x)=3x را بیابید؟
وارون این تابع برابر با f-1(x)=log3x می باشد.
نکته: دامنه تابع لگاریتم logax از شرایط x>0 ، a>0 و a≠1 تبعیت می کند و برد آن R می باشد. به a مبنا گفته خواهد شد.
برای آشنایی با نمودار تابع لگاریتم، می توانید ویدئو آموزشی را مشاهده کنید. برای رسم نمودار تابع لگاریتم، کافی است تابع نمایی یعنی f(x)=ax را نسبت به خط y = x قرینه کنیم. چون تابع لگاریتم، وارون تابع نمایی می باشد.
در تابع لگاریتم y=logax، اگر a > 1 باشد، تابع دارای شرایط زیر است:
- تابع یک به یک است.
- دامنه تابع برابر (∞+,0) و برد آن R است.
- تابع اکیدا صعودی است. یعنی :
x>y ↔ ax>ay
در تابع لگاریتم y=logax ، اگر a بین صفر و یک باشد، تابع دارای شرایط زیر خواهد بود:
- تابع یک به یک است.
- دامنه تابع برابر (∞+,0) و برد آن R است.
- تابع اکیدا نزولی است. یعنی :
x>y ↔ ax<ay
برای رسم نمودار تابع y=log3(x-1)، کافی است نمودار y=log3x را یک واحد به سمت راست انتقال دهیم.
تابع لگاریتم وارون تابع نمایی می باشد.
نمونه تست تابع لگاریتم
به نمونه تست زیر توجه کنید:
تست اول) اگر f(x)=25x-1، ضابطه وارون تابع f کدام است؟
- f-1(x)=log2(5x-1)
- f-1(x)=1+log2x
- f-1(x)=1/5(1+log2x)
- f-1(x)=5+log2x
گزینه 3 پاسخ صحیح می باشد.
برای به دست آوردن ضابطه وارون، باید ابتدا x را بر حسب y به دست آوریم.
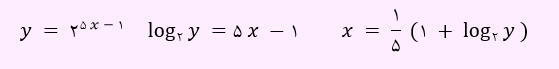
حال جای x و y را عوض نموده و تابع وارون را به دست خواهیم آورد.
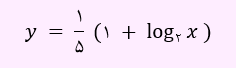
بنابراین تابع وارون به دست آمد.
به نمونه تست دوم دقت کنید:
تست دوم) دامنه تابع f(x)=logx(25-x2) کدام است؟
- (0,5)
- {1}-(0,5)
- {1}-(5,5-)
- (1,5)
گزینه2 پاسخ صحیح می باشد.
برای دامنه این تابع باید شروط زیر برقرار باشد:
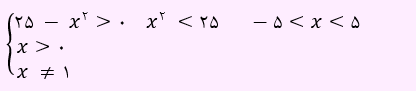
اشتراک سه شرط بالا برابر است با : {1}-(0,5)
به منظور آشنایی با توابع لگاریتمی و نکات مربوط به آن ویدئوی آموزشی این جلسه را مشاهده نمایید.
سوالات متداول
تابع لگاریتم وارون تابع نمایی می باشد.
در تابع لگاریتم y=logax ، اگر a > 1 باشد، آن گاه تابع، اکیدا صعودی می باشد.





