در این فیلم آموزشی در مورد موضوع صفر های تابع، صفرهای تابع درجه دوم و ریشه های تابع توضیح داده شده است.
صفرهای تابع درجه دوم چیست؟
صفرهای تابع درجه 2: نقاط برخورد نمودار تابع مانند f با محور x ها را صفرهای تابع می نامیم که در واقع ریشه های معادل ه f ( x) = 0 هستند.
به نمونه تست های زیر توجه کنید:
تست) معادله سهمی ای رابیابید که 1- سهمی رو به پایین است 2- مقدار صفرهای تابع برابر با 1- و 3 باشد.
- y=-x2+2x+3
- y=-x2-2x+3
- y=x2-3x+2
- y=x2-2x-3
گزینه 1 پاسخ صحیح می باشد.
چون سهمی رو به پایین است، بنابراین ضریب x2 یعنی مقدار a باید منفی باشد. لذا گزینه 3 و 4 غلط خواهد بود.
مقدار صفرهای تابع داده شده اند. بنابراین به ازای صفرهای تابع، مقدار تابع باید صفر شود. مقدار تابع گزینه 2 به ازای x = -1 که صفر تابع است، مخالف صفر و برابر با 4 خواهد شد. بنابراین گزینه 2 نیز غلط می باشد.
به نمونه تست دوم دقت نمائید:
تست) فرض کنید صفرهای یک سهمی به معادله y=ax2+bx+c برابر با 1 و 4 باشد. همچنین سهمی در نقطه 5 محور عرض ها را قطع کند. مقدار ab/c کدام است؟
- 25/16-
- 25/9-
- 5/4-
- 5/3-
گزینه 1 پاسخ صحیح می باشد.
با توجه به اینکه صفرهای سهمی برابر با 1و 4 هستند، پس نمودار سهمی به صورت y=k(x-1)(x-4) می باشد. چون سهمی در نقطه 5 محور عرض ها را قطع می کند، یعنی عرض از مبدا آن 5 بوده و نقطه (0 , 5) در منحنی زیر صدق می کند.
y=k(x-1)(x-4) . بنابراین رابطه زیر را خواهیم داشت.
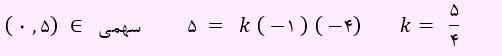
پس معادله سهمی به زیر است.
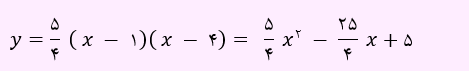
با توجه به معادله بالا، مقدار a برابر با 5/4، b مساوی با 25/4- و c برابر با 5 خواهد شد. لذا حاصل ab/c به صورت زیر به دست می آید.
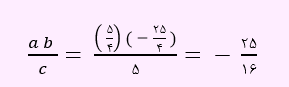
به تست بعدی توجه نمائید:
تست) سهمی به معادله y=ax2+bx+c دارای ریشه مضاعف 2- است. همچنین عرض از مبدا آن 2- می باشد. حاصل a + b + c کدام است؟
- 5/5-
- 2/5-
- 3/5-
- 4/5-
گزینه 4 پاسخ صحیح می باشد.
از آنجایی که سهمی دارای ریشه مضاعف 2- است، بنابراین y آن ضریبی از 2(x+2) می باشد. یعنی
y=k(x+2)2
همچنین عرض از مبدا آن 2- است. لذا نقطه ( 2- , 0) در معادله سهمی صدق می کند.
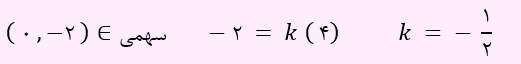
حال معادله سهمی به صورت زیر خواهد شد.
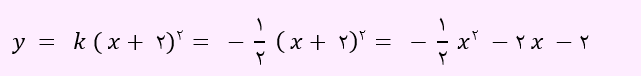
بنابراین مجموع ضرایب یعنی a + b + c برابر با 4/5- خواهد شد.
صفرهای تابع درجه 2، همان ریشه های معادله f(x)=0 می باشند.
برای آشنایی بیشتر با موضوع صفرهای تابع و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
منظور از صفرهای تابع، نقاط تقاطع تابع با محور x ها می باشد. به عبارتی دیگر منظور از صفرهای تابع، ریشه های تابع است.
منظور از ریشه تابع، نقاطی است که مقدار تابع یعنی y به ازای آن ها برابر با صفر خواهد شد.
در یک تابع، منظور از عرض از مبدا نقاطی است که به ازای آن نقاط، مقدار طول یعنی x تابع مساوی با صفر می شود.





