در این فیلم آموزشی به بخش اول فصل دو ریاضی 2 تجربی یعنی عمود منصف و ویژگی های آن خواهیم پرداخت.
عمود منصف پاره خط و ویژگی های آن
عمود منصف یک پاره خط دارای ویژگی های زیر می باشد:
- هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
- هر نقطه که از دو سر یک پاره خط به یک فاصله باشد بر روی عمودمنصف آن پاره خط واقع است.
ویژگی های عمود منصف در شکل زیر نشان داده شده است:

هر نقطه روی عمود منصف یک پاره خط، از دو سر آن پاره خط به یک فاصله است.
نمونه تست عمود منصف پاره خط
در این بخش برای فهم بهتر موضوع به حل نمونه تست می پردازیم.
تست: پاره خط AB به طول CM 10 در شکل مقابل رسم شده است. چند نقطه در صفحه وجود دارد که به فاصلۀ 4 واحد از هر یک از نقاط A و B است؟
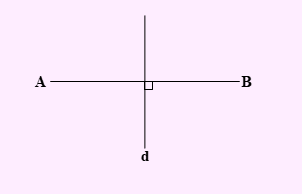
1.یک
2. دو
3. سه
4. بی شمار
گزینه 1 پاسخ صحیح می باشد.
در صورت سوال، نقاطی را می خواهد که به یک فاصله از نقاط A و B باشد. بنابراین نیاز است نقاط خواسته شده روی عمودمنصف قرار داشته باشند. عمود منصف پاره خط را نصف می کند . یعنی فاصله تمام نقاط روی عمودمنصف از نقاط A و B بزرگتر مساوی 5 سانتی متر است. بنابراین هیچ نقطه ای در صفحه وجود ندارد که به فاصله 4 واحد از هر یک از نقاط A و B قرار گرفته باشد.
به نمونه تست دوم دقت نمائید:
تست) در شکل مقابل، چند نقطه در صفحه مثلث ABC وجود دارد که از نقاط A، B و C به یک فاصله باشد؟
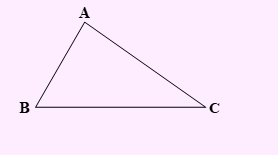
1. یک
2. دو
3. صفر
4. بی شمار
گزینه 1 پاسخ صحیح می باشد.
تمام نقاط روی عمودمنصف پاره خط AB از A و B به یک فاصله است. همچنین تمام نقاط روی عمودمنصف پاره خط AC از A و C به یک فاصله می باشد. نقطه ای که روی تقاطع عمود منصف دو پاره خط AB و AC وجود دارد از نقاط A، B و C به یک فاصله می باشد. بنابراین در صفحه تنها یک نقطه وجود دارد که از نقاط A، B و C به یک فاصله باشد. به این نقطه مرکز دایره محیطی مثلث گفته می شود.
به منظور یادگیری بیشتر موضوع عمودمنصف پاره خط و ویژگی های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
عمودمنصف یک پاره خط، مکان هندسی نقاطی است که از دو سر پاره خط به یک فاصله می باشد.
مرکز دایره محیطی یک مثلث، نقطه ای است که اگر دایره به مرکز این نقطه و شعاع (فاصله از این نقطه تا یکی از رئوس مثلث) زده شود، از تمام رئوس مثلث خواهد گذشت. در واقع، در صفحه تنها یک نقطه وجود دارد که از تمام رئوس مثلث به یک فاصله باشد، به این نقطه مرکز دایره محیطی مثلث گفته خواهد شد.
هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک فاصله است.





