در این فیلم آموزشی با موضوع قضیه میانه ها در هندسه و نکات مهم کنکوری آن آشنا خواهید شد.
قضیه میانه ها
در مثلث ABC با اندازه های اضلاع a، b و c همواره بین طول میانه ها و اضلاع روابط زیر برقرار است. به این روابط قضیه میانه ها گفته خواهد شد.

قضیه میانه ها روابط بین طول میانه ها و اضلاع را بیان می کند.
نمونه تست قضیه میانه ها
به نمونه تست زیر دقت کنید:
تست: در مثلث ABC با طول سه میانۀ ma، mb و mc حاصل (a2+b2+c2)/(ma2+mb2+mc2) کدام است؟
1- 4/5
2- 3/4
3- 2/3
4- 1
پاسخ : گزینه 2 پاسخ صحیح می باشد.
ابتدا رابطه طولی بین میانه ها و اضلاع را سه مرتبه می نویسیم. سپس سه رابطه را با هم جمع خواهیم کرد. در واقع داریم:

به نمونه تست دوم در مورد موضوع قضیه میانه ها توجه فرمایید:
تست: در مثلث ABC، اندازه BC=√6، AC=2 و میانۀ CM برابر 10/2√ است. مساحت این مثلث چقدر است؟

1- 10√
2- 6√2
3- 6√
4- 10√2
پاسخ : گزینه 3 پاسخ صحیح می باشد.
ابتدا رابطه قضیه میانه ها را برای ضلع C می نویسیم. سپس اندازه های داده شده را در رابطه جایگذاری می کنیم.
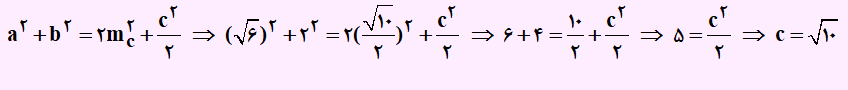
بعد از به دست آمدن ضلع C متوجه می شویم که مثلث ABC یک مثلث قائم الزاویه است. در نهایت مساحت مثلث قائم الزاویه را طبق رابطه به دست می آوریم:

برای یادگیری بیشتر موضوع قضیه میانه ها و نکات کنکوری آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
قضیه میانه ها روابط بین طول میانه ها و اضلاع را بیان می کند. در واقع قضیه میانه ها می گوید مجموع توان دوم دو ضلع برابر است با مجموع دو برابر توان دوم میانه ضلع دیگر و نصف توان دوم ضلع دیگر.
قضیه میانه ها روابط بین طول میانه ها و اضلاع را بیان خواهد کرد.





