در این فیلم آموزشی، به موضوع سهمی، ماکزیمم و مینیمم سهمی خواهیم پرداخت.
ماکزیمم و مینیمم سهمی
سهمی: نمودار تابع y=ax2+bx+c یک سهمی است (a≠0) . نمودار تابع سهمی در صورتی که a >0 با شد، رو به بالاست و اگر a < 0 باشد، نمودار آن رو به پایین می باشد. مختصات راس سهمی به صورت زیر است .

در حالتی که سهمی رو به بالاست، به راس سهمی مینیمم و در حالتی که سهمی رو به پایین است، به راس آن ماکزیمم گفته می شود.
به نمونه مثال زیر توجه کنید:
مثال: کمترین مقدار تابع f(x)=2x2-4x+1 چقدر است؟
منظور از کمترین مقدار تابع، کمترین مقدار عرض های آن تابع خواهد بود. در این مثال چون a > 0 است، سهمی رو به بالا می باشد. پس باید عرض راس سهمی که مینیمم است را بیابیم.
در ابتدا مقدار x راس سهمی را یافته و سپس آن را در معادله قرار می دهیم تا مقدار y یعنی عرض راس سهمی به دست آید.
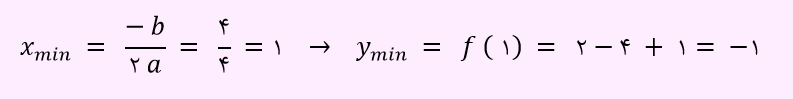
بنابراین کمترین مقدار تابع برابر با 1- به دست آمد.
در نمودار سهمی، در حالتی که سهمی رو به بالاست به راس سهمی مینیمم گفته خواهد شد.
نمونه تست ماکزیمم و مینیمم سهمی
در این بخش به منظور درک بهتر موضوع ماکزیمم و مینیمم سهمی چند نمونه تست حل می کنیم.
تست) اگر 3x+y=6 ، بیشترین مقدار x y چقدر است؟1
- 5/2
- 3/2
- 3
- 4
گزینه 3 پاسخ صحیح می باشد.
از تساوی بالا، y را بر حسب x به صورت زیر به دست می آوریم.
y=6-3x
حال به جای y، در حاصل x y ، مقدار به دست آمده را قرار خواهیم داد.
xy=x(6-3x)=-3x2+6x
حال باید بیشترین مقدار تابع بالا رابیابیم.
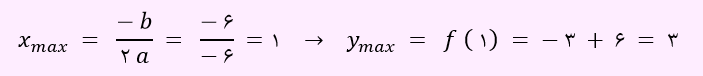
بنابراین گزینه 3 درست است.
به نمونه تست دوم توجه کنید:
تست) اگر نقطه A( 1, 2) نقطه ماکزیمم تابع f(x)=-x2+ax+b باشد، حاصل a b کدام است؟
- 3/2
- 2
- 3
- 4/3
گزینه 2 پاسخ صحیح می باشد.
اولا A( 1, 2) باید در تابع صدق کند.
(1,2)∈f -1+a+b=2 a+b=3
ثانیا این نقطه، ماکزیمم سهمی است، بنابراین رابطه زیر را خواهیم داشت.
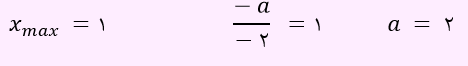
لذا مقدار b برابر با یک و حاصل a b مساوی با 2 خواهد شد.
به منظور یادگیری بیشتر موضوع ماکزیمم و مینیمم سهمی ویدئو آموزشی را مشاهده کنید.
سوالات متداول
تابع y = ax2 + b x+ c معادله یک سهمی است( a ≠0). نمودار این تابع در حالتی که a کوچکتر از صفر باشد، رو به پایین بوده و سهمی دارای ماکزیمم می باشد. در حقیقت در این حالت، راس سهمی نقطه ماکزیمم است.
تابع y = ax2 + b x+ c یک سهمی می باشد( a ≠0). نمودار این تابع در حالتی که a بزرگتر از صفر باشد، رو به بالا است و سهمی دارای مینیمم است. در واقع در این حالت، راس سهمی نقطه مینیمم می باشد.






ح
عالب