در این فیلم آموزشی با پیشامدهای مستقل، وابسته و نکات آن آشنا خواهید شد.
پیشامدهای مستقل و وابسته
پیشامدهای مستقل: دو پیشامد A و B را مستقل گوییم هر گاه وقوع هر یک در احتمال وقوع دیگری هیچ تاثیری نداشته باشد. در واقع دو پیشامد A و B مستقل اند اگر و فقط اگر P(A∩B)=P(A)×P(B). اگر A و B مستقل نباشند، آن گاه وابسته اند.
مثال) در پرتاب 2 تاس با هم، پیشامد A برآمد عدد 3 در تاس اول و پیشامد B مجموع برآمدها 7 است. آیا دو پیشامد مستقل هستند؟
بله. پیشامدهای A ، B و A∩B به صورت زیر خواهند بود:
A={(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)}
B={(1,6),(12,5),(3,4),(4,3),(5,2),(6,1)}
A ∩B={(3,4)}
بنابراین احتمال پیشامدهای A ، B و A∩B به شکل زیر است:
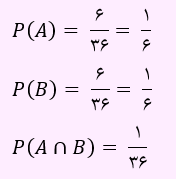
P(A∩B)=P(A)×P(B) است. بنابراین دو پیشامد A و B مستقل می باشند.
نکته: اشتراک دو پیشامد مستقل هیچ گاه تهی نخواهد شد. توجه شود دو پیشامد ناسازگار و مستقل با یکدیگر تفاوت دارند.
نکته: اگر A و B دو پیشامد مستقل باشند، آن گاه پیشامدهای زیر نیز مستقل اند:
1- ‘A و B
2- A و ‘B
3- ‘A’ , B

مثال) احتمال قبولی علی در درس آمار و احتمال 90 درصد و احتمال قبولی محمد در همان درس 70 درصد است. احتمال این که حداقل یکی از آن ها قبول شود چقدر است؟
احتمال قبولی علی را P(A) و احتمال قبولی محمد را P(B) در نظر می گیریم. صورت سوال P(A∪B) را خواسته است. بنابراین داریم:
قبول شدن علی و محمد به یکدیگر ارتباطی ندارد. بنابراین این دو پیشامد مستقل هستند و احتمال اشتراک آن ها برابر با حاصل ضرب احتمال هر کدام است. یعنی داریم:
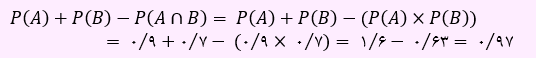
لذا احتمال اینکه حداقل یکی از آن ها قبول شود، برابر با 0.97 به دست آمد.
دو پیشامد مستقل پیشامدهایی هستند که وقوع هر یک در وقوع دیگری هیچ تاثیری نداشته باشد.
نمونه تست پیشامد مستقل و وابسته
حال برای آشنایی با تست های کنکور سراسری به حل تست خواهیم پرداخت.
تست اول) احتمال موفقیت عمل پیوند کلیه روی یک بیمار 0.6 و روی بیمار دیگری 0.8 است. اگر این عمل روی هر دو نفر انجام گیرد، نسبت احتمال موفقیت هر دو عمل به شکست هر دو عمل چقدر است؟
الف) 6
ب) 2
ج) 3
د) 8
گزینه الف پاسخ صحیح می باشد.
احتمال موفقیت عمل پیوند کلیه روی یک بیمار 0.6 را P(A) و دیگری را P(B) در نظر می گیریم. دو پیشامد مستقل از یکدیگر هستند. لذا داریم:
چون دو پیشامد مستقل هستند. متمم آن ها (یعنی شکست آن ها) نیز مستقل خواهد بود. احتمال شکست هر دو عمل به صورت زیر محاسبه خواهد شد:
سوال نسبت این دو احتمال، یعنی نسبت احتمال موفقیت هر دو عمل به شکست هر دو عمل را خواسته است. لذا داریم:
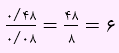
به تست بعدی دقت کنید:
تست دوم) در گروه زنان ساکن یک روستا 60 درصد تحصیلات ابتدایی و 25 درصد مهارت قالیبافی دارند. اگر یک نفر از میان آن ها انتخاب شود با چه احتمالی تحصیلات ابتدایی یا مهارت قالیبافی دارد؟
الف) 0.7
ب) 0.75
ج) 0.8
د) 0.85
گزینه الف پاسخ صحیح می باشد.
احتمال داشتن تحصیلات ابتدایی را P(A) و داشتن مهارت قالیبافی را P(B) در نظر می گیریم. سوال P(A∪B) را خواسته است. همچنین دو پیشامد مستقل هستند. بنابراین داریم:
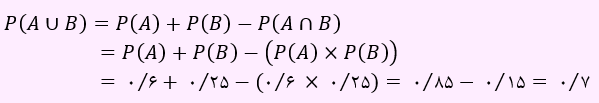
لذا نفر انتخابی با احتمال 0.7 دارای تحصیلات ابتدایی یا مهارت قالیبافی خواهد بود.
برای فهم بیشتر موضوع پیشامدهای وابسته، مستقل و تست های آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
فرض کنید A و B دو پیشامد باشند، آن گاه دو پیشامد A و B را مستقل گوییم هر گاه وقوع هر یک در احتمال وقوع دیگری هیچ تاثیری نداشته باشد.
بله. فرض کنید A و B دو پیشامد مستقل باشند، در آن صورت متمم های آن ها یعنی ‘A و ‘B نیز با یکدیگر مستقل خواهند بود.
خیر. اشتراک دو پیشامد مستقل هیچ گاه تهی نخواهد شد. در واقع دو پیشامد مستقل حتما با یکدیگر اشتراک خواهند داشت.





