در این ویدئو آموزشی با مبحث یاقتن کوچکترین مضرب مشترک دو چند جمله ای و نمونه سوالات تستی آن آشنا خواهید شد.
یافتن کوچکترین مضرب مشترک دو چند جمله ای
برای پیدا کردن کوچکترین مضرب مشترک دو چند جمله ای مراحل زیر را طی می کنیم:
1- اولین قدم برای یافتن کوچکترین مضرب مشترک دو چند جمله ای این است که دو چند جمله ای را تجزیه کنیم.
2- عبارت های مشترک و غیر مشترک را مشخص می کنیم.
3- حاصل ضرب عبارت های مشترک با بزرگترین توان را در عبارات غیر مشترک، به دست می آوریم.
در مثال زیر می توانید مراحل گفته شده را به ترتیب مشاهده کنید:

اولین قدم در یافتن کوچکترین مضرب مشترک دو چند جمله ای، تجزیه دو چند جمله ای است.
نمونه تست کوچکترین مضرب مشترک دو چند جمله ای
به نمونه تست زیر در مورد کوچکترین مضرب مشترک دو چند جمله ای(ک.م.م) دقت کنید:
تست) کوچکترین مضرب مشترک P(x)=x2+x و Q(x)=(x2-1)(x+1) کدام است؟
1- x(x+1)(x-1)
2- x(x+1)2(x-1)
3- x(x+1)(x-1)2
4- (x+1)2(x-1)2
پاسخ : گزینه 2 پاسخ صحیح می باشد.
P(x)=x2+x=x(x+1)
Q(x)=(x2-1)(x+1)=(x-1)(x+1)2
مشترک x+1
غیر مشترک x, (x-1)
ک.م.م= (x+1)2×x×(x-1)
ابتدا دو عبارت را تجزیه کرده ایم. برای تجزیه عبارت اول از x فاکتور گرفته ایم و برای تجزیه عبارت دوم از اتحاد مزدوج استفاده کرده ایم. سپس عامل های مشترک و غیر مشترک را نوشته و در نهایت کوچکترین مضرب مشترک دو چند جمله ای برابر با x(x+1)2(x-1) به دست خواهد آمد.
به نمونه تست دوم توجه فرمایید:
تست) اگر کوچکترین مضرب مشترک P(x)=x2+x و q(x)=x2-1 را A(x) بنامیم، حاصل A(x)/Q(x) کدام است؟
1- x
2- x-1
3- x+1
4- 1
پاسخ : گزینه 1 پاسخ صحیح می باشد.
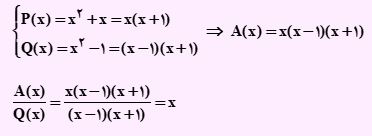
ابتدا دو عبارت را تجزیه می کنیم. در تجزیه عبارت اول از x فاکتور گرفته و در تجزیه عبارت دوم از اتحاد مزدوج استفاده کردیم. عامل مشترک x و عامل غیر مشترک x, x-1 است. پس ک.م.م که برابر A(x) است به دست آمد. سپس با جایگذاری حاصل مقدار خواسته شده را به دست خواهیم آورد.
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع کوچکترین مضرب مشترک دو چند جمله ای به ویدئو آموزشی مراجعه کنید.
سوالات متداول
اولین قدم به منظور پیدا کردن کوچکترین مضرب مشترک دو چند جمله ای این است که دو چند جمله ای را تجزیه کنیم.
به منظور یافتن کوچکترین مضرب مشترک دو چند جمله ای مراحل زیر را طی می کنیم:
1- هر دو چند جمله ای را تجزیه می کنیم.
2- عبارت های مشترک و غیر مشترک را مشخص می کنیم.
3- حاصل ضرب عبارت های مشترک با بزرگترین توان را در عبارات غیر مشترک، به دست می آوریم.





