در این فیلم آموزشی با قضیه زیر مجموعه ها در جبر گزاره ها آشنا خواهید شد.
قضیه: برای هر دو مجموعه دلخواه A و B از مجموعه مرجع U داریم:
A ⊆ B ⇔ {A ∩ B = AA ∪ B ∪ B = B
تست اول) اگر A ∪ (B – A) = B، آن گاه کدام گزینه درست است؟
- A ⊆ B
- B ⊆ A
- A = Ø
- B = Ø
گزینه 1 پاسخ صحیح می باشد.
این مسئله را با نمودار ون به صورت زیر حل خواهیم کرد:
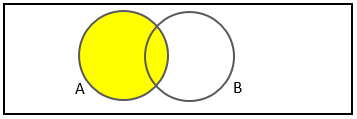

در تصویر بالا مجموعه A زرد رنگ شده است و B – A سفید رنگ است. بنابراین A ∪ (B – A) طبق نمودار ون برابر با A ∪ B خواهد بود. یعنی داریم:
A ∪ (B – A) = A ∪ B = B
لذا طبق رابطه بالا، A ⊆ B می باشد.
تست دوم) اگر A ⊆ B آن گاه مجموعه A’ ∩ B) ∪ (A ∩ B’) ∪ (A ∩ B)) برابر کدام گزینه است؟
- A
- B
- ‘A
- ‘B
گزینه 2 پاسخ صحیح می باشد.
(A’ ∩ B) را به صورت زیر می توان نوشت.
A’ ∩ B) = (B ∩ A’) = (B – A))
(‘A ∩ B) را نیز می توان به شکل زیر نوشت:
A ∩ B’) = A – B)
بنابراین عبارت بالا به شکل زیر خواهد بود:
B – A) ∪ (A – B) ∪ (A ∩ B))
حال با توجه به نمودار ون داریم:


در نمودار ون، (َA – B) با هاشور نارنجی رنگ، (B – A) با دایره های توپر مشکی و (A ∩ B) با مثلث های زرد رنگ مشخص شده اند. با توجه به نمودار ون حاصل عبارت B – A) ∪ (A – B) ∪ (A ∩ B)) برابر با A ∪ B می باشد. با توجه به اینکه A ⊆ B است، حاصل A ∪ B مساوی با B خواهد شد.
نکته: برای هر دو مجموعه دلخواه A و B از مجموعه مرجع U داریم:
‘A ⊆ B ⇔ B’ ⊆ A
تست سوم) اگر ‘B’ ⊆ A آن گاه مجموعه A – B) ∪ (B – A) ∪ (A ∩ B)) برابر کدام گزینه است؟
- A
- B
- ‘A
- ‘B
گزینه 2 پاسخ صحیح می باشد.
با توجه به اینکه ‘B’ ⊆ A آن گاه A ⊆ B خواهد بود. با توجه به تست قبلی، حاصل A – B) ∪ (B – A) ∪ (A ∩ B)) برابر با A ∪ B می باشد و چون A ⊆ B است، حاصل A ∪ B مساوی با B خواهد بود.
تست چهارم) اگر ‘B’ ⊆ A آن گاه مجموعه A ∩ (B – C)) – (A ∩ B ∩ C)) برابر کدام گزینه است؟
- A – C
- A ∩ C
- A
- B
گزینه 1 پاسخ صحیح می باشد.
اگر ‘B’ ⊆ A باشد آن گاه A ⊆ B است. عبارت A ∩ (B – C)) – (A ∩ B ∩ C))، را به صورت زیر ساده خواهیم کرد:
A ∩ (B -C)) – (A ∩ B ∩ C) = ( A ∩ B ∩ C’) – (A ∩ B ∩ C))
چون A ⊆ B است، حاصل A ∩ B برابر با خواهد بود. بنابراین داریم:
A ∩ B ∩ C’ – (A ∩ B ∩ C) = (A ∩ C’) – (A ∩ C) = A ∩ (C’ – C)
با توجه به اینکه دو مجموعه C و ‘C هیچ اشتراکی ندارند. حاصل عبارت بالا برابر با ‘A ∩ C یعنی A – C خواهد شد.
فرض کنید A و B دو مجموعه دلخواه از مجموعه مرجع U باشد و مجموعه A زیر مجموعه B باشد، آن گاه برای اجتماع آن ها رابطه زیر را داریم:
A ⊆ B ⇔ A ∪ B = B
فرض کنید A و B دو مجموعه دلخواه از مجموعه مرجع U باشد و مجموعه A زیر مجموعه B باشد، آن گاه برای اشتراک آن ها رابطه زیر را خواهیم داشت:
A ⊆ B ⇔ A ∩ B = A
فرض کنید A و B دو مجموعه دلخواه از مجموعه مرجع U باشند و مجموعه A زیر مجموعه B باشد ، آن گاه داریم:
‘A ⊆ B ⇔ B’ ⊆ A




