در این فیلم آموزشی در مورد مبحث مثلثات بخش انواع زاویه های مثلثاتی(درجه و رادیان)، محاسبه طول کمان مقابل به زاویه رادیان و مساحت قطاع توضیح داده شده است.
واحدهای اندازه گیری زاویه درجه و رادیان
به منظور اندازه گیری زاویه از واحدهای رادیان و درجه می توان استفاده نمود.
درجه: اگر محیط دایره ای را به 360 کمان مساوی تقسیم کنیم، اندازه زاویه مرکزی رو به روی هر کدام از این کمان ها ” ا درجه” است.
رادیان: ” 1 رادیان” برابر است با اندازه زاویه مرکزی دایره ای که طول کمان رو به روی آن با شعاع دایره مساوی است.
تبدیل درجه به رادیان: اگر اندازه زاویه ای بر حسب درجه D و برحسب رادیان R باشد، داریم:


مثال) Π/36 رادیان چند درجه است؟
برای تبدیل این زاویه به درجه می توان از رابطه بیان شده استفاده نمود.
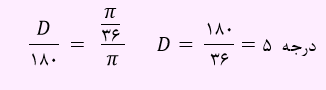
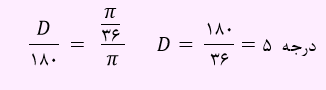
به مثال دوم توجه کنید:
مثال) 24 درجه معادل چند رادیان است؟
بدین منظور از رابطه زیر استفاده خواهیم کرد:
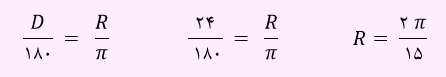
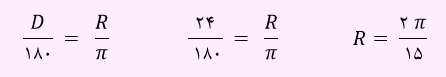
رادیان و درجه دو نمونه از واحدهای اندازه گیری زاویه می باشند.
نمونه تست واحدهای اندازه گیری زاویه
به نمونه تست زیر توجه کنید:
تست) مجموع اندازه های دو زاویه بر حسب درجه برابر 22/5 درجه و اختلاف اندازه های آن ها بر حسب رادیان برابر 7Π/72 است. اندازه زاویه بزرگتر بر حسب رادیان کدام است؟
- Π/9
- Π/6
- Π/8
- Π/12
گزینه 1 پاسخ صحیح می باشد.
فرض کنیم دو زاویه x و y باشند. بنابراین روابط زیر را خواهیم داشت:
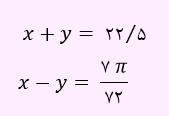
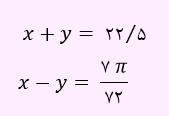
چون زاویه بزرگتر را بر حسب رادیان خواسته، ابتدا 22/5 درجه را بر حسب رادیان به دست می آوریم.
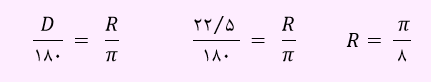
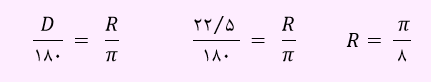
لذا روابط قبلی به صورت زیر بر حسب رادیان خواهند شد.
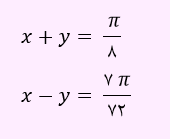
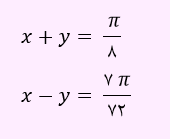
از جمع دو رابطه بالا نتیجه می شود:
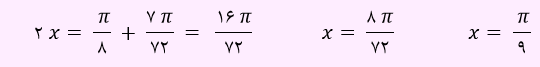
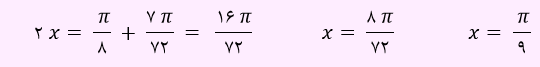
پس اندازه زاویه بزرگتر برابر با Π/9 به دست آمد.
نکته: توجه کنید که هر یک رادیان به صورت تقریبی معادل 57 درجه است.
به نمونه تست دوم توجه کنید:
تست) کدام یک از موارد زیر بیانگر یک عدد حقیقی منفی است؟
- sin3
- cos6
- tan2
- cot4
گزینه 3 پاسخ صحیح می باشد.
هنگامی که علامت درجه گذاشته نمی شود، منظور رادیان است.
منظور از sin3 ، عدد 3 رادیان است. یعنی 3 رادیان 57×3 معادل 171 درجه می باشد. بنابراین در ربع دوم قرار دارد که مقدار سینوس در این ربع مثبت است. cos6 یعنی 57×6 که برابر با 342 درجه می باشد. بنابراین در ربع چهارم قرار خواهد گرفت که کسینوس در این ربع مثبت خواهد بود. tan2 معادل با 57×2 یعنی 114 درجه می باشد. این زاویه در ربع چهارم قرار می گیرید و تانژانت در این ربع منفی خواهد بود. پس مقدار گزینه 3 یک عدد حقیقی منفی است.
نکته: در دایره ای به شعاع R، طول کمان مقابل به زاویه θ رادیان از رابطه زیر محاسبه می شود:
L=Rθ
در دایره ای به شعاع R، مساحت قطاع به زاویه مرکزی θ رادیان برابر است با:
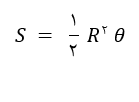
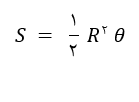
برای آشنایی بیشتر با واحد اندازه گیری زوایای مثلثاتی و پاسخ به تست های کنکور آن ویدئوی آموزشی این جلسه را مشاهده نمایید.
سوالات متداول
واحدهای اصلی به منظور اندازه گیری زاویه دو واحد شامل درجه و رادیان می باشند. برای اندازه گیری زاویه از این دو واحد می توان استفاده نمود.
برای تبدیل زاویه بر حسب درجه به رادیان باید اندازه زاویه بر حسب درجه را بر 180 تقسیم نموده و با اندازه زاویه بر حسب رادیان تقسیم بر عد پی برابر قرار دهیم تا تناسب ایجاد شود. سپس از این تناسب اندازه زاویه بر حسب رادیان محاسبه خواهد شد.




