پیوستگی در بازه چیست؟

صفحه اصلی

محتوای آموزشی

پایه یازدهم

پیوستگی در بازه چیست؟

در این فیلم آموزشی به موضوع پیوستگی بر بازه و تعداد نقاط ناپیوسته روی یک بازه خواهیم پرداخت.

پخش ویدئو

پیوستگی بر بازه

در ابتدا به حل چند نمونه تست در مورد موضوع پیوستگی می پردازیم.

تست) اگر تابع زیر، در x = 0 فقط پیوستگی چپ داشته باشد، a کدام است؟

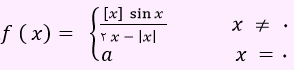
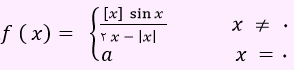
1
1-
1/3-
صفر

گزینه 3 پاسخ صحیح می باشد.

ابتدا حد چپ را پیدا می کنیم.

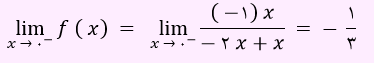
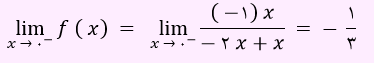
با توجه به رابطه بالا، مقدار تابع در نقطه x = 0 باید برابر با 1/3- باشد. بنابراین مقدار a مساوی با 1/3- است. لذا گزینه 3 پاسخ صحیح می باشد.

در این مثال عبارت ” وجود ندارد” جز گزینه ها نیست، بنابراین نیاز به محاسبه حد راست برای بررسی اینکه حد وجود دارد، نمی باشد. برای یادگیری بیشتر، حد راست نیز به صورت زیر محاسبه خواهد شد.

لذا حد راست برابر با صفر و حد چپ مساوی با 1/3- شد.

پیوستگی بر بازه به چهار بخش زیر تقسیم می شود:

f بر (a,b) پیوسته است هر گاه در هر نقطه از بازه (a,b) پیوسته باشد.
f بر (a,b] پیوسته است هر گاه در هر نقطه از بازه (a,b) پیوسته باشد و در x=a پیوستگی راست داشته باشد.
f بر [a,b) پیوسته است هر گاه در هر نقطه از بازه (a,b) پیوسته باشد و در x=b پیوستگی چپ داشته باشد.
f را بر [a,b] پیوسته گوییم هر گاه در a پیوستگی راست و در b پیوستگی چپ داشته باشد و در تمام نقاط بازه پیوسته باشد.

به طور مثال y=(x²-3x+2)[x] در بازه (0,3] پیوسته است

زیرا، ابتدا تابع را به صورت زیر تجزیه خواهیم کرد.

y=(x-1)(x-2)[x]

اگر تابع در نقطه صفر پیوستگی راست داشته باشد و در نقاط 1 و 2 پیوسته باشد، تابع در بازه (0,3]پیوسته خواهد بود.

بنابراین حد تابع را در نقاط مذکور محاسبه خواهیم کرد.

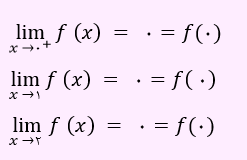
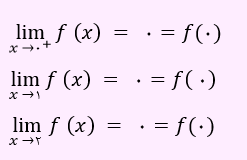
لذا تابع f در x = 2 پیوسته می باشد. تابع مذکور در سایر نقاط نیز پیوسته خواهد بود. بنابراین تابع در بازه (0,3] پیوسته است.

یکی از راه ها برای یافتن تعداد نقاط ناپیوسته بر روی یک بازه، رسم نمودار تابع می باشد. برای آشنایی بیشتر با این موضوع و حل نمونه تست ها ویدئو آموزشی را مشاهده کنید.

به منظور آشنایی بیشتر با موضوع پیوستگی بر بازه و نمونه سوالات تستی آن ویدئو آموزشی را مشاهده کنید.