در این فیلم آموزشی، مبحث جملات مشترک دو دنباله حسابی آموزش داده شده است.
جملات مشترک دو دنباله حسابی
دو دنباله حسابی اگر یک جمله مشترک داشته باشند، آنگاه بی شمار جمله مشترک خواهند داشت به طوری که قدر نسبت جملات مشترک ک . م .م قدر نسبت های دو دنباله حسابی خواهد بود. حال به حل یک مثال می پردازیم.
مثال: با توجه به دو دنباله حسابی زیر
2, 9, 16, 23, …
12, 17, 22, 27, ….
نهمین جمله مشترک چه عددی است؟
دنباله حسابی اول دارای قدرنسبت 7 و دنباله حسابی دوم دارای قدرنسبت 5 می باشد.
برای پاسخ به سوال، ابتدا نیاز است اولین جمله مشترک را پیدا کنیم.
برای یافتن اولین جمله مشترک یا باید جملات را به قدری بنویسیم تا به اولین جمله مشترک برسیم یا جمله عمومی دنباله اول را با جمله عمومی دنباله دوم مساوی قرار داد. در ابتدا جملات را به قدری می نویسیم تا به اولین جمله مشترک برسیم.
2, 19, 16, 23, 30, 37, ….
12, 17, 22, 27, 32, 37, …
بنابراین اولین جمله مشترک برابر با 37 خواهد شد. لذا d جملات مشترک از طریق رابطه زیر به دست می آید.
d = [7, 5]=35
پس قدر نسبت جملات مشترک از طریق ک . م .م عدد 35 به دست آمد.
بنابراین در ادامه از طریق رابطه زیر، نهمین جمله مشترک را به دست می آوریم.
cn=c1+(n-1)d=37+35(n-1)=35n+2
c9=35×9+2=317
لذا نهمین جمله مشترک برابر با 317 خواهد بود.
دو دنباله حسابی در صورت داشتن یک جمله مشترک دارای بی شمار جمله مشترک خواهند بود.
نمونه تست جملات مشترک دو دنباله حسابی
حال در ادامه برای یادگیری بیشتر موضوع به حل یک تست خواهیم پرداخت.
تست) اعداد طبیعی را به صورت …,{6, 5, 4}, {3, 2}, {1} دسته بندی کرده ایم. جمع جملات در دسته بیستم چه عددی است؟
- 4010
- 4020
- 4030
- 4040
گزینه 1 پاسخ صحیح می باشد.
برای جمع جملات این دسته ها، روابط زیر را خواهیم داشت:
{1} 1= جمع جملات
{2, 3} 5= جمع جملات
{4, 5, 6} 15 = جمع جملات
برای دسته ها رابطه زیر را خواهیم داشت. در واقع در دسته اول، یک عدد مصرف شد، در دسته دوم دو عدد و در دسته سوم سه عدد مصرف شد. بنابراین در دسته 19 ام، 19 عدد مصرف خواهد شد.
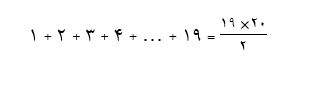
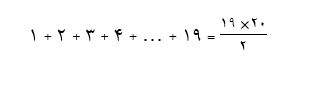
لذا تا دسته 19 ام، 190 عدد طبیعی به کار رفت. بنابراین دسته 20 ام با 191 آغاز و دارای بیست عدد خواهد شد.
{…, 192, 191} =دسته بیستم
در دسته بیستم قدر نسبت برابر با 1، جمله اول مساوی 191 و n برابر با 20 می باشد. پس s20 از طریق رابطه زیر به دست خواهد آمد.
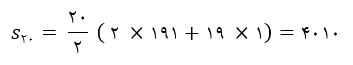
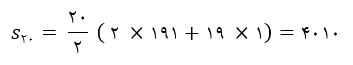
بنابراین جمع جملات در دسته بیستم برابر با 4010 می شود. لذا گزینه یک پاسخ صحیح است.
به منظور یادگیری بیشتر موضوع جملات مشترک دو دنباله حسابی و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
برای پیدا کردن اولین جمله مشترک، یک روش این است که جملات را به قدری بنویسیم تا اولین جمله مشترک دو دنباله حسابی را بیابیم یا روش دوم این است که جمله عمومی دنباله اول را با جمله عمومی دنباله دوم برابر قرار دهیم و اولین جمله مشترک دو دنباله را پیدا کنیم.
برای محاسبه قدر نسبت جملات مشترک دو دنباله حسابی که دارای جملات مشترک هستند، باید ک . م .م قدر نسبت های دو دنباله حسابی را حساب نمود.
برای اینکه دریابیم یک دنباله حسابی است، نیاز است دو جمله متوالی را از هم کم نمائیم، اگر به عدد ثابتی برسیم، در این صورت دنباله مورد نظر، یک دنباله یا تصاعد حسابی می باشد.





چگونه ثابت می کنید قدر نسبت دنباله جملات مشترک برابر ک.م.م قدر نسبت دو دنباله است؟